
Location: Artus Contemporary Art Studio (Budapest, H)
Format: Algorithmic Installation. Thermal Printer, Paper, Sound
Year: 2019
Description
A thermal printer and a microcontroller generates lines of an image on a stripe of paper, infinitely. The printer and the controller are mounted on top of a loudspeaker. The delay time is different between each printed line, that results to an organic rythym that never repeats itself. Since the sound of the printer is amplified, it also generates a minimalistic percussion-like soundscape. The endless image is a discrete model: a one dimensional cellular automata with varying rules in its evolution. The paper stripe forms an ever growing heap on the ground during the whole exhibition.
Cells and their lifecycle
A cellular automaton is a system consisting of cells of numerical values on a grid, together with a rule that decides the behaviour of these cells. By applying the rule repeatedly on each cell in the grid while visualising the grid in some way or another, one often gets the effect of some evolving organism with complex and intricate behavior, even from relatively simple rules.
In mathematics and computability theory, an elementary cellular automaton is a one-dimensional cellular automaton where there are two possible states (labeled 0 and 1) and the rule to determine the state of a cell in the next generation depends only on the current state of the cell and its two immediate neighbors. As such it is one of the simplest possible models of computation. Nevertheless, there is an elementary cellular automaton which is capable of universal computation.
00011110
Rule 30 is an elementary cellular automaton introduced by Stephen Wolfram in 1983. Using Wolfram's classification scheme, Rule 30 is a Class III rule, displaying aperiodic, chaotic behaviour.
This rule is of particular interest because it produces complex, seemingly random patterns from simple, well-defined rules. Because of this, Wolfram believes that Rule 30, and cellular automata in general, are the key to understanding how simple rules produce complex structures and behaviour in nature. For instance, a pattern resembling Rule 30 appears on the shell of the widespread cone snail species Conus textile.
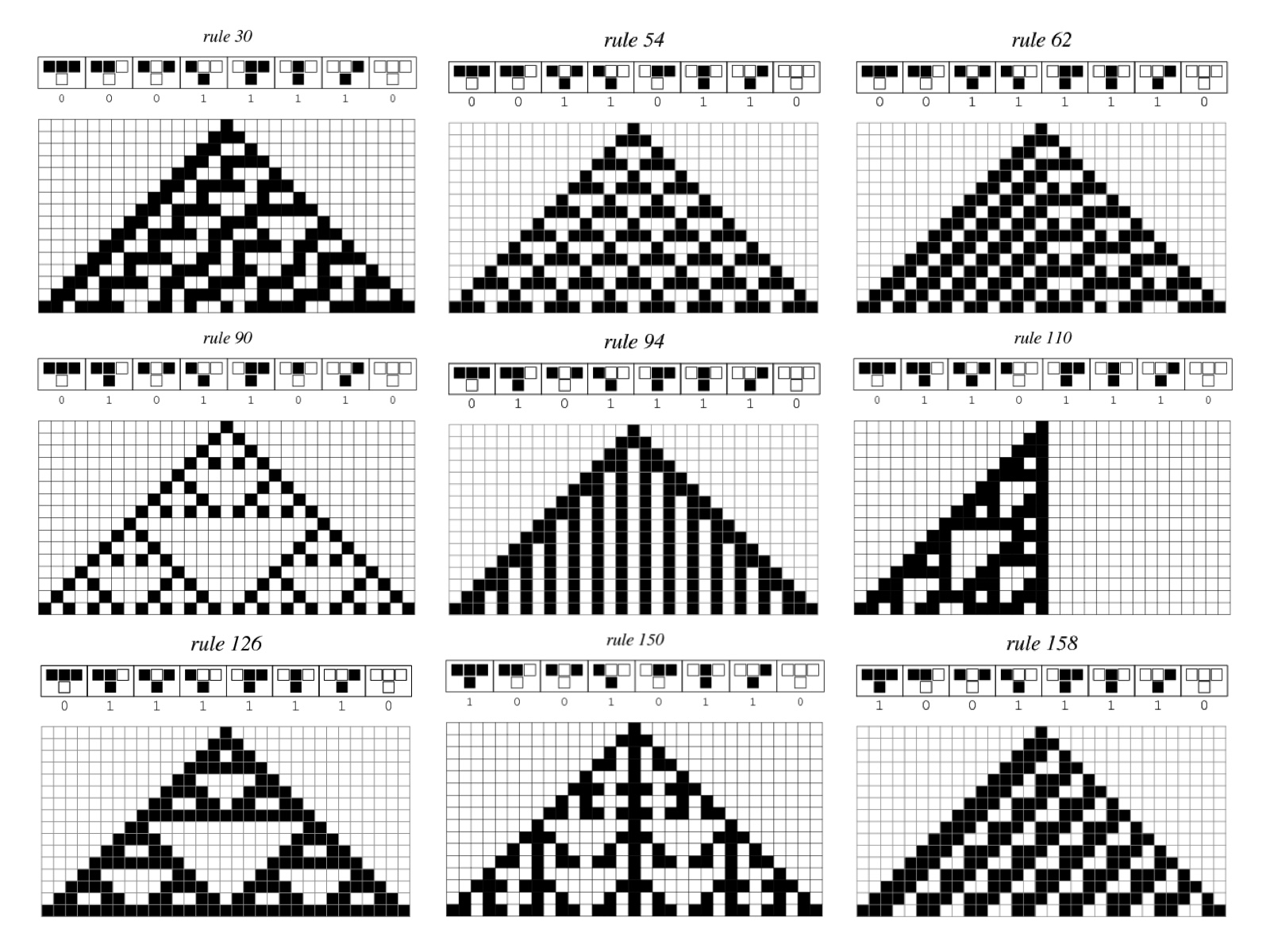 Each number between 0 and 255 directly corresponds to an ECA (Elementary Cellular Automaton ) rule, and is thus used to name the rules. Any number in the interval from 0 through 255 can be represented in binary using only 8 digits.
Each number between 0 and 255 directly corresponds to an ECA (Elementary Cellular Automaton ) rule, and is thus used to name the rules. Any number in the interval from 0 through 255 can be represented in binary using only 8 digits.

The installation is an automated entity that is experiencing the different trajectories of this simulation in realtime.

turning a thermalprinter into an audiovisual sequencer, by generating 1D #cellular #automata on an #arduino & delaying each printing line with different timing #creativecoding pic.twitter.com/H046KpxOWZ
— agoston nagy (@_stc) October 6, 2019
Binaura © 2025